Cómo obtener la función inversa de una función

¿Qué es una función inversa?

Una función inversa es aquella que "revierte" los efectos de la función original. Si \( y = f(x) \) es la función original, su inversa \( f^{-1}(y) \) es la función que cumple:

Esto significa que si aplicamos \( f \) a un valor \( x \) y luego aplicamos la inversa \( f^{-1} \) al resultado, volveremos al valor inicial \( x \).

Ejemplo básico

Si \( f(x) = x + 2 \), la función inversa de \( f \) es \( f^{-1}(x) = x - 2 \). Esto se debe a que:

y de manera similar:

Condiciones para que una función tenga inversa

No todas las funciones tienen inversa. Para que una función \( f \) tenga una inversa, debe cumplir las siguientes condiciones:

1. Ser inyectiva: La función debe ser tal que cada valor de salida (rango) esté asociado con un único valor de entrada (dominio). En otras palabras, no puede haber dos valores distintos de \( x \) que den el mismo valor de \( y \).

2. Ser biyectiva: Esto significa que la función debe ser tanto inyectiva como suprayectiva (que todos los valores posibles en el rango son alcanzados por al menos un valor del dominio).

Una forma fácil de verificar si una función tiene inversa es mediante la prueba de la línea horizontal: si cada línea horizontal corta a la gráfica de la función en, como máximo, un punto, entonces la función tiene inversa.

Pasos para calcular la función inversa

Para encontrar la función inversa de \( f(x) \), sigue estos pasos:

1. Reemplazar \( f(x) \) por \( y \): Esto te ayudará a trabajar con la ecuación más fácilmente.

2. Intercambiar \( x \) y \( y \): Cambia las posiciones de \( x \) y \( y \) en la ecuación para reflejar la relación inversa.

3. Despejar \( y \): Resuelve la ecuación para \( y \). Este nuevo valor de \( y \) será la función inversa.

4. Reemplazar \( y \) por \( f^{-1}(x) \): La expresión que obtuviste en el paso anterior es la inversa de \( f \).

Veamos este procedimiento con un ejemplo.

Ejemplo: Encontrar la inversa de \( f(x) = 2x + 3 \)

1. Reemplazar \( f(x) \) por \( y \):

2. Intercambiar \( x \) y \( y \):

3. Despejar \( y \):

4. Reemplazar \( y \) por \( f^{-1}(x) \):

La función inversa de \( f(x) = 2x + 3 \) es:

Ejemplos de funciones con y sin inversa

1. Función con inversa: \( f(x) = x^3 \)

Esta función es inyectiva y biyectiva, ya que para cada valor de \( y \), existe exactamente un valor de \( x \) tal que \( f(x) = y \).

2. Función sin inversa: \( f(x) = x^2 \)

La función cuadrática no tiene inversa porque no es inyectiva. Por ejemplo, tanto \( f(2) = 4 \) como \( f(-2) = 4 \). Para que esta función tenga una inversa, necesitamos restringir su dominio a \( x \geq 0 \).

Dominio y rango de la función inversa

El dominio de la función original \( f \) se convierte en el rango de su función inversa \( f^{-1} \) y viceversa. Si la función original tiene un dominio \( D \) y un rango \( R \), entonces la función inversa tendrá el dominio \( R \) y el rango \( D \).

Ejemplo

Para la función \( f(x) = 2x + 3 \), el dominio es \( (-\infty, \infty) \) y el rango también es \( (-\infty, \infty) \). La inversa \( f^{-1}(x) = \frac{x - 3}{2} \) tiene el mismo dominio y rango.

Si tienes una función más complicada, asegúrate de determinar estos conjuntos antes de encontrar la inversa, especialmente si restringes el dominio para hacer la función inyectiva.

Gráficas de funciones inversas

La gráfica de una función y su inversa son simétricas respecto a la línea \( y = x \). Esto significa que si doblas el plano a lo largo de la línea \( y = x \), la gráfica de la función y la de su inversa se superpondrán.

Ejemplo gráfico

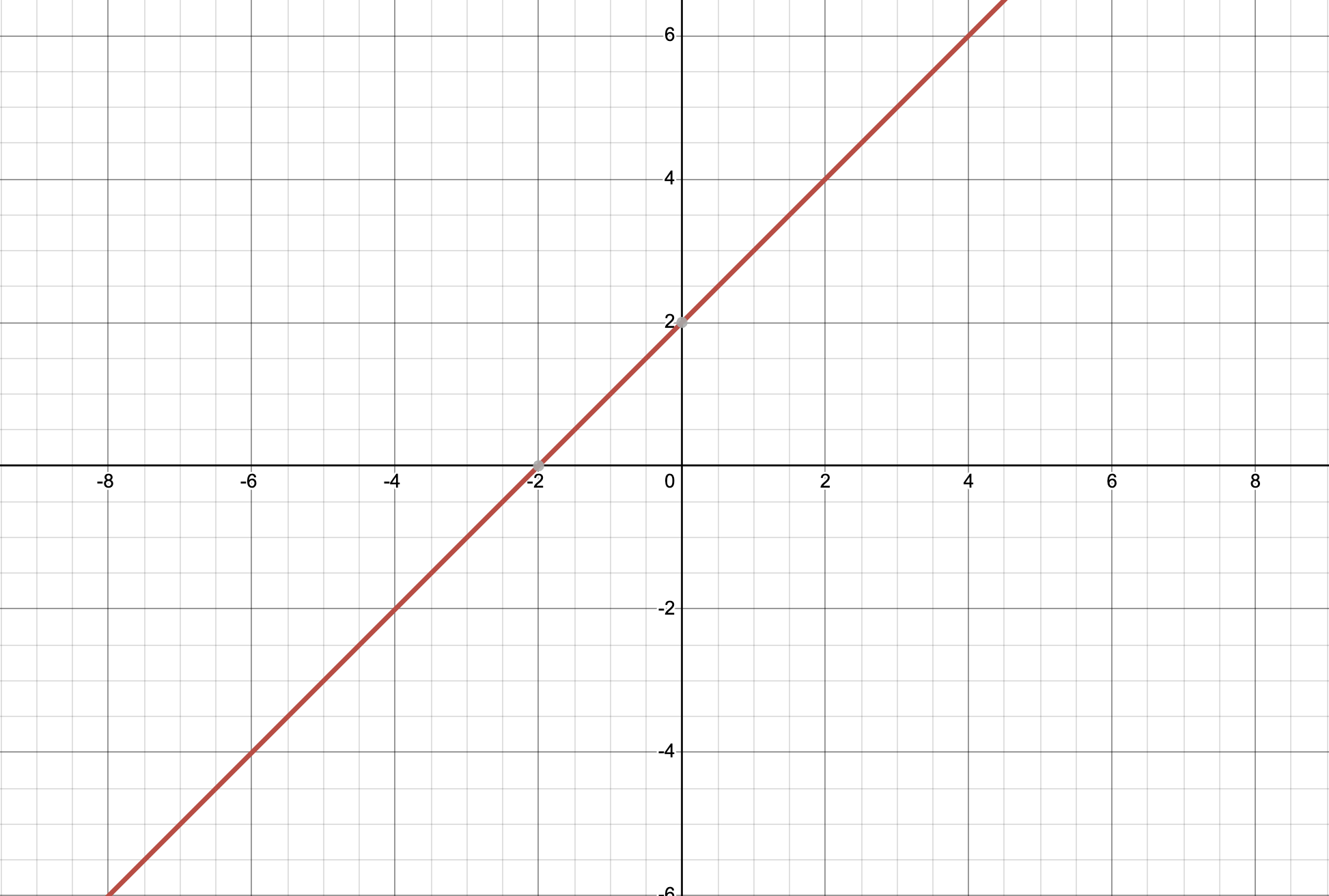
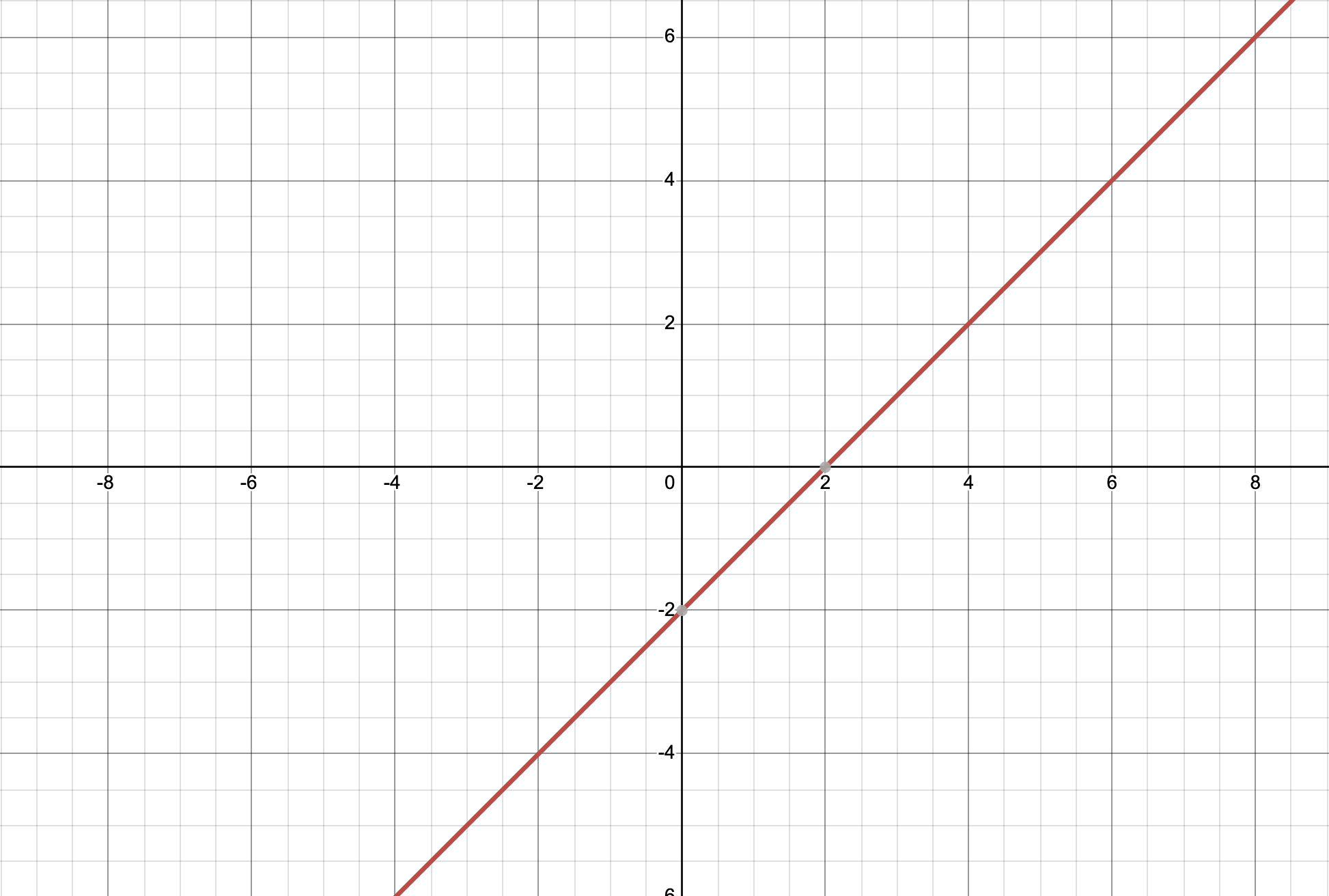
Si dibujas la función \( f(x) = x + 2 \) y su inversa \( f^{-1}(x) = x - 2 \), verás que sus gráficas se reflejan en la línea \( y = x \).